Regression in Python

August 24, 2018
python
PDSH
regression

Linear and Polynomial Regression

Here’s some cool initial code from page 378 (under “Derived Features” in the section on Feature Engineering) in the Python Data Science Handbook (PDSH). This code will allow me to quickly fit a linear and polynomial regression to very simple data. My comments are marked something like ### GJL::

% matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1,2,3,4,5])
y = np.array([4,2,1,3,7])
plt.scatter(x,y)  ### GJL: uses the function scatter() from matplotlib.pyplot. In R this call would look like plt::scatter(X,y)

<matplotlib.collections.PathCollection at 0x1a1f7ec400>

png

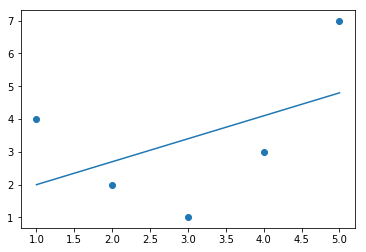
Now they do linear regression using the package (is it called a package in Python?) LinearRegression. These will be good lines to dissect for learning Python. I have to be absolutely fluent in stuff like this. Note, to understand the line X = x[:, np.newaxis] line, see here.

from sklearn.linear_model import LinearRegression
X = x[:, np.newaxis] ### GJL: turns x into a column vector for use in LinearRegression().fit().
model = LinearRegression().fit(X,y)    
yfit = model.predict(X)
plt.scatter(x,y)
plt.plot(x, yfit);

png

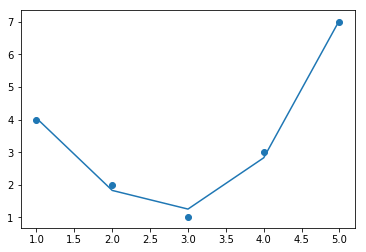
Now they do polynomial regression:

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3, include_bias=False)  ### GJL: My guess is "include bias" means "include intercept"
X2 = poly.fit_transform(X)
print(X2)

[[  1.   1.   1.]
 [  2.   4.   8.]
 [  3.   9.  27.]
 [  4.  16.  64.]
 [  5.  25. 125.]]

Now we do linear regression on this modified input.

### GJL: notice I'm overwriting the `model` variable. In this notebook, chronological type presentation, the variable names should serve mostly as educational tools in the reader's mind -- so no need to have e.g. model1, model2, model3, etc.
model = LinearRegression().fit(X2,y)  
yfit = model.predict(X2)
plt.scatter(x, y)
plt.plot(x, yfit)

[<matplotlib.lines.Line2D at 0x1a1f8cd128>]

png

Final thought

The book closes this linear and polynomial regression example with a nice final thought:

“This idea of improving a model not by changing the model, but by transforming the inputs, is fundamental to many of the more powerful machine learning methods. We explore this idea further in “In Depth: Linear Regression” in the context of basis function regression. More generally, this is one motivational path to the powerful set of techniques known as kernel methods, which we will explore in “In-Depth: Support Vector Machines”.